- Avtor Jason Gerald [email protected].
- Public 2024-01-15 08:23.
- Nazadnje spremenjeno 2025-01-23 12:45.
Vrednost P je statistična meritev, ki znanstvenikom pomaga ugotoviti, ali je njihova hipoteza pravilna. Vrednost P se uporablja za ugotavljanje, ali so rezultati njihovega poskusa v območju vrednosti, ki so normalne za proučevane stvari. Običajno, če vrednost P nabora podatkov pade pod določeno vnaprej določeno vrednost (na primer 0,05), bodo znanstveniki zavrnili ničelno hipotezo svojega poskusa - z drugimi besedami, izključili bodo hipotezo, kjer ima eksperimentalna spremenljivka brez pomembnega vpliva na rezultat. Danes se vrednosti p običajno nahajajo v referenčnih tabelah z izračunom vrednosti hi na kvadrat.
Korak

Korak 1. Določite pričakovane rezultate vašega poskusa
Običajno, ko znanstveniki izvedejo poskus in pregledajo rezultate, že vnaprej razumejo normalne ali običajne rezultate. To lahko temelji na rezultatih prejšnjih poskusov, zanesljivih nizih opazovalnih podatkov, znanstveni literaturi in/ali drugih virih. Za svoj poskus določite pričakovani rezultat in ga zapišite kot številko.
Primer: Predpostavimo, da je prejšnja študija pokazala, da so bile na nacionalni ravni karte za prehitro vožnjo izdane rdečim avtomobilom kot modrim avtomobilom. Recimo, da povprečni rezultat na nacionalni ravni kaže razmerje 2: 1, pri čemer je razmerje rdečih avtomobilov večje. Ugotoviti želimo, ali ima tudi policija v našem mestu enako težnjo z analizo kazni za prehitro vožnjo, ki jo je izdala policija v našem mestu. Če bi vzeli naključni vzorec 150 vozovnic za prehitro vožnjo za rdeče in modre avtomobile v našem mestu, bi pričakovali 100 za rdeč avto in 50 za modre avtomobile, če policijska enota v našem mestu podari vozovnico glede na primerjavo na državni ravni.

Korak 2. Določite svoja eksperimentalna opazovanja
Zdaj, ko ste določili pričakovano vrednost, lahko zaženete poskus in poiščete pravo vrednost (ali opazovanje). Še enkrat zapišite rezultat kot številko. Če manipuliramo z nekaterimi eksperimentalnimi pogoji in se opaženi rezultati razlikujejo od pričakovanih, obstajata dve možnosti: bodisi se je to zgodilo po naključju, bodisi je naša razlika z eksperimentalnimi spremenljivkami povzročila to razliko. Namen ugotavljanja p-vrednosti je v bistvu ugotoviti, ali se opazovani rezultati razlikujejo od pričakovanih do točke, ko nične hipoteze-hipoteze, da med eksperimentalno spremenljivko in razmerjem ni opaziti-ni mogoče zavrniti.
Primer: Recimo, da v našem mestu naključno izberemo 150 vozovnic za prehitro vožnjo, ki jih prejmejo rdeči in modri avtomobili. Dobimo 90 vozovnico za rdeč avto in 60 za modri avto. To se razlikuje od rezultata, ki smo ga pričakovali, tj 100 in 50. Ali je naša eksperimentalna manipulacija (v tem primeru spreminjanje vira podatkov iz državnega v lokalno) povzročila kakršno koli spremembo rezultatov ali pa je imela naša mestna policija enake težnje kot nacionalna raven in smo opazili le naključje? Vrednost p nam bo pomagala določiti.

Korak 3. Določite stopnje svobode za vaš poskus
Stopnje svobode so merilo količine variabilnosti v študiji, ki je določena s številom kategorij, ki jih preučujete. Enačba za stopnje svobode je Stopnje svobode = n-1, kjer je n število kategorij ali spremenljivk, analiziranih v vašem poskusu.
-
Primer: Naš poskus ima dve kategoriji rezultatov: enega za rdeči avto in drugega za modrega avtomobila. Tako imamo v našem poskusu 2-1 = 1 stopnja svobode.
Če primerjamo rdeče, modre in zelene avtomobile, jih bomo imeli
2. korak. stopnje svobode itd.

Korak 4. Primerjajte pričakovane rezultate z opaženimi rezultati s pomočjo hi -kvadrata
Chi na kvadrat (napisano x2) je številska vrednost, ki meri razliko med pričakovanimi in opaženimi vrednostmi iz poskusa. Enačba za chi na kvadrat je: x2 = ((o-e)2/e), kjer je o opazovana vrednost in e pričakovana vrednost. Rezultate te enačbe seštejte za vse možne rezultate (glejte spodaj).
- Upoštevajte, da ta enačba uporablja operator (sigma). Z drugimi besedami, izračunati morate ((| o-e | -,05)2/e) za vsak možni izid nato seštejte rezultate, da dobite vrednost hi na kvadrat. V našem primeru imamo dva rezultata - avto, ki dobi rdečo ali modro vozovnico. Tako lahko izračunamo ((o-e)2/e) dvakrat - enkrat za rdeči avto in enkrat za modri avto.
-
Primer: Priključimo pričakovane vrednosti in opažanja v enačbo x2 = ((o-e)2/e). Ne pozabite, da moramo zaradi operaterja sigma izračunati ((o-e)2/e) dvakrat - enkrat za rdeči avto in enkrat za modri avto. Koraki obdelave so naslednji:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Korak 5. Izberite raven pomembnosti
Zdaj, ko vemo stopnje svobode našega eksperimentalnega kompleta in vrednost hi na kvadrat, moramo narediti še eno stvar, preden lahko najdemo svojo vrednost p-določiti moramo stopnjo pomembnosti. V bistvu je raven pomembnosti merilo, kako prepričani smo v svoje rezultate - nizka stopnja pomembnosti ustreza majhni verjetnosti, da je bil rezultat poskusa posledica naključja in obratno. Raven pomembnosti je zapisana kot decimalka (npr. 0,01), kar ustreza odstotni verjetnosti, da je bil rezultat poskusa posledica naključja (v tem primeru 1%).
- Po dogovoru znanstveniki običajno določijo vrednost pomembnosti za svoje poskuse na 0,05 ali 5 odstotkov. To pomeni, da imajo eksperimentalni rezultati, ki ustrezajo tej stopnji pomembnosti, največ 5% možnosti naključja. Z drugimi besedami, obstaja 95% verjetnost, da so rezultati posledica znanstvenikove manipulacije eksperimentalnih spremenljivk in ne naključja. Za večino poskusov je 95 -odstotno zaupanje v razmerje med dvema spremenljivkama uspešno dokazano.
- Primer: Za naš primer rdeče -modrega avtomobila sledimo znanstvenemu dogovoru in določimo stopnjo pomembnosti 0, 05.
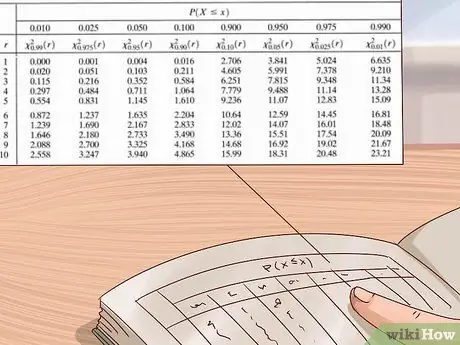
Korak 6. Uporabite tabelo porazdelitve hi kvadrat za oceno vaše p-vrednosti
Znanstveniki in statistiki uporabljajo velike tabele vrednosti za izračun vrednosti p za svoje poskuse. Ta tabela je običajno napisana z navpično osjo na levi strani, ki prikazuje stopnje svobode, in vodoravno osjo na vrhu, ki prikazuje vrednosti p. Uporabite to tabelo tako, da najprej poiščete stopnje svobode, nato pa berete vrstice od leve proti desni, dokler ne najdete prve vrednosti, ki je večja od vaše vrednosti chi na kvadrat. Poglejte p-vrednost na vrhu stolpca-vaša p-vrednost je med to vrednostjo in naslednjo največjo vrednostjo (desna vrednost je levo od nje).
- Razpredelnice Chi kvadrat so na voljo iz različnih virov - zlahka jih najdete na spletu ali v učbenikih o znanosti ali statistiki. Če ga nimate, uporabite tabelo, prikazano na zgornji fotografiji, ali brezplačno spletno mizo, kot je na primer medcalc.org tukaj.
-
Primer: Naš chi na kvadrat je 3. Zato uporabimo tabelo porazdelitve chi kvadrat na zgornji fotografiji, da poiščemo približno vrednost p. Ker vemo, da ima naš poskus le
Korak 1. stopnje svobode, bomo začeli z zgornje tabele. V tej vrstici gremo od leve proti desni, dokler ne najdemo vrednosti, višje od
3. korak. - naša vrednost chi na kvadrat. Prva vrednost, ki jo najdemo, je 3,84. Če pogledamo ta stolpec, vidimo, da je ustrezna vrednost p 0,05. To pomeni, da je naša vrednost p med 0,05 in 0,1 (naslednja največja vrednost p v tabeli).

Korak 7. Odločite se, ali boste svojo ničelno hipotezo zavrnili ali zagovarjali
Ker ste našli približno vrednost p za vaš poskus, se lahko odločite, ali želite zavrniti ničelno hipotezo vašega poskusa (ne pozabite, da je to hipoteza, da eksperimentalna spremenljivka, s katero ste manipulirali, ni vplivala na rezultate, ki ste jih opazili). Če je vaša vrednost p nižja od vrednosti pomembnosti, čestitam-dokazali ste, da obstaja velika verjetnost, da obstaja povezava med spremenljivkami, s katerimi ste manipulirali, in vašimi opažanji. Če je vaša vrednost p večja od vrednosti vašega pomena, ne morete z gotovostjo trditi, da so rezultati, ki jih opazujete, zgolj naključje ali manipulacija vašega poskusa.
- Primer: Naša vrednost p je med 0,05 in 0,1. To pomeni, da nikakor ni manjša od 0,05, zato smo na žalost ne more zavrniti naše ničelne hipoteze. To pomeni, da ne dosežemo minimalne meje zaupanja 95%, ki smo jo določili, tako da je mogoče reči, da policija v našem mestu daje vozovnice za rdeče in modre avtomobile v razmerju, ki je precej drugačno od državnega povprečja.
- Z drugimi besedami, obstaja 5-10% verjetnost, da naša opažanja niso posledica spremembe lokacije (analiziramo naše mesto in ne celotnega dela), ampak so naključja. Ker iščemo verjetnost, manjšo od 5%, ne moremo reči, da smo prepričan da policija v našem mestu ponavadi kupuje rdeče avtomobile - obstaja majhna, a statistično zelo različna možnost, da te tendence nimajo.
Nasveti
- Znanstveni kalkulator bo izračune precej olajšal. Kalkulatorje lahko iščete tudi na spletu.
- Vrednosti p lahko izračunate z več računalniškimi programi, vključno s pogosto uporabljeno programsko opremo za preglednice in bolj specializirano statistično programsko opremo.






