Vzajemnost ali vzajemnost je zelo uporabna pri vseh vrstah algebrskih enačb. Na primer, ko delite en ulomek na drugega, pomnožite prvi ulomek z recipročno vrednostjo drugega. Pri iskanju enačbe črte morate uporabiti tudi obratno.
Korak
Metoda 1 od 3: Iskanje inverze ulomka ali celega števila
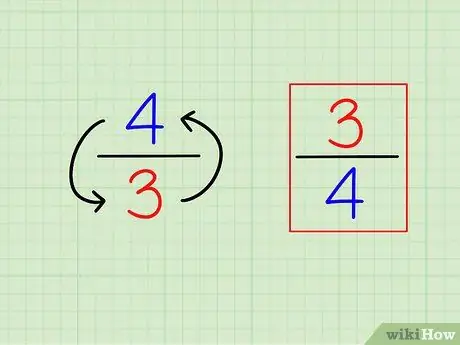
Korak 1. Poiščite vzajemnost ulomka tako, da ga obrnete
Opredelitev "vzajemnosti" ali nasprotno je zelo enostavna. Če želite najti vzajemnost katerega koli celega števila, preprosto izračunajte "1 (to število)". Za ulomke je vzajemnost drugačen ulomek, to je, da so številke "obrnjene" (obratno).
- Na primer, nasprotno od 3/4 je 4/3.
- Vsako število, pomnoženo z vzajemnimi donosi 1.
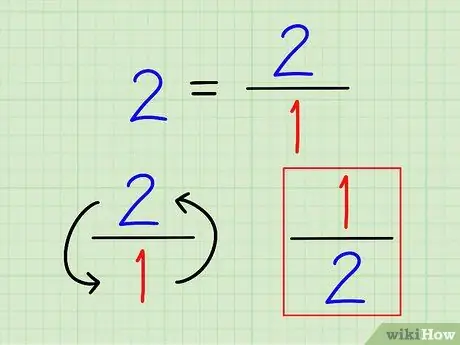
Korak 2. Zapišite vzajemnost celotnega števila kot ulomek
Spet je vzajemnost števila vedno 1 (to število). Za cela števila jih zapišite kot ulomke. Tega števila nima smisla izračunati na decimalko.
Na primer, recipročna vrednost 2 je 1 2 = 1/2.
Metoda 2 od 3: Iskanje inverza mešanega ulomka
Korak 1. Opredelite mešane številke
Mešane ulomke sestavljajo cela števila in ulomki, na primer 24/5. Obstajata dva koraka za iskanje vzajemnosti mešanega števila, kot je opisano spodaj.
Korak 2. Pretvorite mešana števila v nepravilne ulomke
Ne pozabite, da je 1 vedno mogoče zapisati kot (število)/(isto število), ulomke z istim imenovanikom (spodnja številka) pa lahko seštejemo. Tu je primer uporabe 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
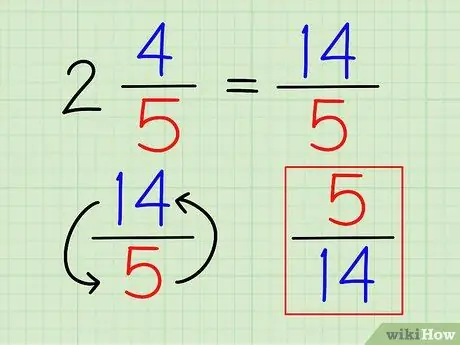
Korak 3. Obrnite ulomek
Ko je številka v celoti zapisana kot ulomek, lahko z obračanjem ulomka ugotovite njeno vzajemnost tako kot kateri koli drug ulomek.
V zgornjem primeru je vzajemnost od 14/5 je 5/14.
Metoda 3 od 3: Iskanje nasprotja decimalnega mesta
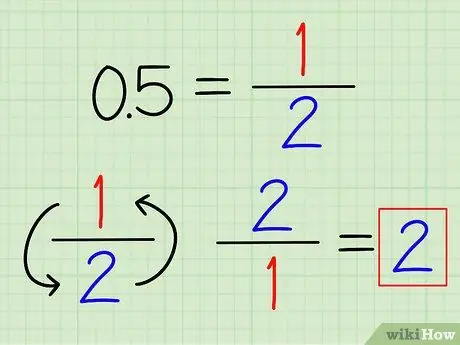
Korak 1. Pretvorite decimalke v ulomke, če je mogoče
Morda boste prepoznali nekaj pogosto uporabljenih decimalnih števil, ki jih je mogoče enostavno pretvoriti v ulomke. Na primer, 0,5 = 1/2 in 0,25 = 1/4. Ko je decimalni del pretvorjen v ulomek, ga preprosto obrnite, da poiščete njegovo vzajemnost.
Na primer, recipročna vrednost 0,5 je 2/1 = 2.
Korak 2. Napišite problem delitve
Če je ne morete pretvoriti v ulomek, izračunajte recipročno vrednost števila v obliki problema deljenja: 1 (decimalno). Za rešitev lahko uporabite kalkulator ali pa ročno rešite naslednji korak.
Na primer, lahko dobite vzajemno vrednost 0,4 z izračunom 1 0,4
Korak 3. Spremenite deljenje problema tako, da uporabite cela števila
Prvi korak pri deljenju decimalk je premikanje decimalne vejice, dokler niso vse številke cela števila. Dokler premikate decimalno vejico obeh številk za enako število korakov, boste dobili pravi odgovor.
Na primer, lahko uporabite 1 0, 4 in ga prepišete kot 10 4. V tem primeru premaknete vsa decimalna mesta za en korak v desno, enako pomnožite vsako število z desetimi
Korak 4. Rešite težavo z dolgim deljenjem
Za izračun vzajemnosti uporabite metodo dolge delitve. Če štejete 10 4, boste dobili odgovor 2, 5 ki je vzajemna vrednost 0, 4.
Nasveti
- Negativni povratni vložek števila je enak običajnemu vzajemnemu, saj se pomnoži z negativnim. Na primer, negativna vzajemnost 3/4 je -4/3.
- Vzajemnost ali vzajemnost se pogosto imenuje "obratno množenje".
- Številka 1 je nasprotna sama sebi, ker je 1 1 = 1.
- Število 0 nima vzajemnosti, ker 0 ni določeno.
