- Avtor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:23.
- Nazadnje spremenjeno 2025-01-23 12:44.
Dodajanje in odštevanje ulomkov je pomembna spretnost. Delci se v vsakdanjem življenju pojavljajo ves čas, zlasti pri pouku matematike, od osnovne šole do fakultete. Sledite tem korakom, če želite izvedeti, kako seštevati in odštevati ulomke iz enakovrednih, neenakih ulomkov, mešanih številk ali skupnih ulomkov. Če že poznate en način, je res enostavno rešiti druge ulomke!
Korak
Metoda 1 od 4: seštevanje in odštevanje ulomkov z istim imenovalcem
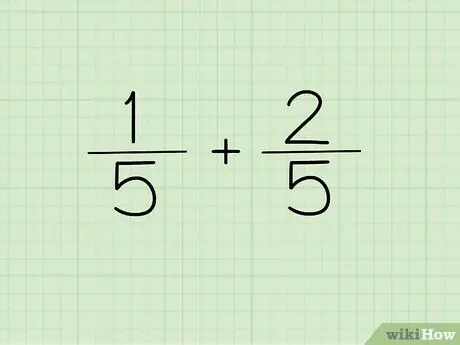
Korak 1. Zapišite svoje vprašanje
Če je imenovalec dveh ulomkov, ki jih želite dodati ali odšteti, enak, zapišite imenovalnik enkrat kot imenovalec svojega odgovora.
Z drugimi besedami, 1/5 in 2/5 ni treba zapisati kot 1/5 + 2/5 =?, vendar se lahko zapiše kot (1+2)/5 =?. Imena so enaka, zato jih je mogoče zapisati le enkrat. Dva števca sta združena
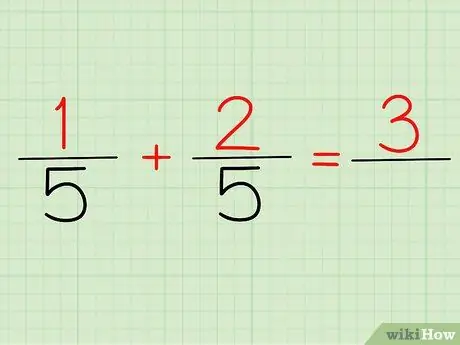
Korak 2. Seštejte števce
Števec je število, ki je nad katerim koli ulomkom. Če pogledamo zgornji problem, so 1/5 in 2/5, 1 in 2 naši števci.
Ne glede na to, ali ga napišete 1/5 + 2/5 ali (1 + 2)/5, bo vaš odgovor enak: 3! Ker je 1 + 2 = 3

Korak 3. Pustite imenovalec
Ker so imenovalci enaki, ne delajte ničesar z imenovalci! Ne seštevajte, odštevajte, množite ali delite. Naj bo.
Torej je iz istega primera naš imenovalec 5. Prav! 5 je najnižja številka našega ulomka. Imamo polovico odgovora

4. korak Zapišite svoj odgovor
Zdaj morate le zapisati svoj števec in imenovalec! Če uporabite zgornji primer, bo vaš odgovor 3/5.
Kakšen je tvoj števec? 3. Vaš imenovalec? 5. Zato je 1/5 + 2/5 ali (1 + 2)/5 enako 3/5.
Metoda 2 od 4: seštevanje in odštevanje ulomkov z različnimi imenovalci

Korak 1. Poiščite najmanjši skupni imenovalec
To pomeni, da je najmanjši imenovalec enak za oba ulomka. Recimo, da imamo ulomke 2/3 in 3/4. Kaj je imenovalec? 3 in 4. Če želite najti najmanjši skupni imenovalec obeh ulomkov, lahko to storite na tri načine:
- Zapišite večkratnike. Večkratniki 3 so 3, 6, 9, 12, 15, 18 … itd. Večkratniki 4? 4, 8, 12, 16, 20 itd. Katero je najmanjše število, ki je večkratnik obeh? 12! To je najmanj skupni imenovalec.
-
Osnovna faktorizacija. Če poznate dejavnike, lahko naredite primarno faktorizacijo. To pomeni, da iščete številke, ki sestavljajo vaš imenovalec. Za številko 3 sta faktorja 3 in 1. Za številko 4 sta faktorja 2 in 2. Nato vsi. 3 x 2 x 2 = 12. Vaš najmanj skupni imenovalec!
Pomnožite vse številke za manjše število. V nekaterih težavah, kot je ta, lahko pomnožite obe številki - 3 x 4 = 12. Če pa imate velik imenovalec, tega ne storite! Ne želite pomnožiti 56 x 44 in se potruditi, da dobite 2464

Korak 2. Pomnožite imenovalec s številom, ki je potrebno, da dobite najmanjši skupni imenovalec
Z drugimi besedami, želite, da so vsi vaši imenovalci enaki. V našem primeru želimo, da je imenovalec 12. Če želite spremeniti 3 v 12, pomnožite 3 s 4. Če želite spremeniti 4 v 12, pomnožite 4 s 3. Isti imenovalec bo imenovalec vašega končnega odgovora.
-
Tako 2/3 postane 2/3 x 4 in 3/4 postane 3/4 x 3. To pomeni, da imamo zdaj 2/12 in 3/12. Ampak, še nismo končali!
- Opazili boste, da se imenovalci med seboj pomnožijo. To je mogoče storiti v tej situaciji, vendar ne v vseh situacijah. Včasih lahko namesto množenja obeh imenovalcev oba imenovalca pomnožite z drugo številko, da dobite manjše število.
- Pri drugih težavah morate včasih samo pomnožiti en imenovalec, da bo enak imenovalec drugega ulomka v nalogi.

Korak 3. Pomnožite števec z isto številko
Ko imenovalec pomnožite s številom, morate tudi števec pomnožiti z istim številom. Kar smo naredili v zadnjem koraku, je le del množenja, ki ga je treba narediti.
Za prvi korak imamo 2/3x4 in 2/4x3 - nato pa v drugem koraku 2 x 4/3 x 4 in 3 x 3/4 x 3. To pomeni, da so naše nove številke 8/12 in 9/ 12. Popolno
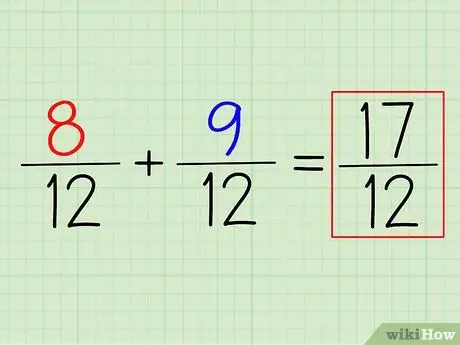
Korak 4. Dodajte (ali odštejte) števce, da dobite odgovor
Če želite dodati 8/12 + 9/12, morate samo dodati števce. Ne pozabite: pustite imenovalec. Najmanjši skupni imenovalec, ki ga najdete, je vaš končni imenovalec.
V tem primeru je (8+9)/12 = 17/12. Če ga želite pretvoriti v mešano število, samo odštejte imenovalec od števca in zapišite preostanek. V tem primeru je 17/12 = 1 5/12
Metoda 3 od 4: Dodajanje in odštevanje mešanih in običajnih ulomkov
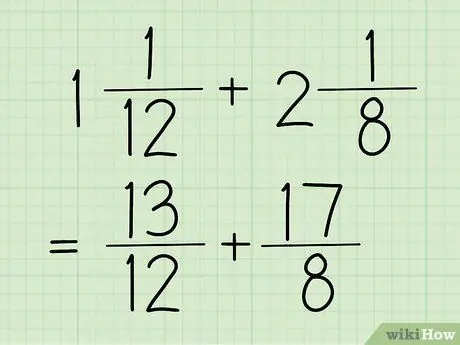
Korak 1. Pretvorite mešane ulomke v običajne
Mešano število je ulomek, ki ima celo število in ulomek, kot v zgornjem primeru (1 5/12). Medtem je navaden ulomek ulomek, katerega števec (zgornja številka) je večji od imenovalca (spodnje število). Ta del je viden tudi v prejšnjem koraku, ki je 17/12.
Za primere v tem razdelku bomo uporabili 13/12 in 17/8

Korak 2. Poiščite skupni imenovalec
Se spomnite treh načinov, kako najti najmanj skupni imenovalec? S pisanjem večkratnikov, z uporabo osnovne faktorije ali množenjem imenovalcev.
Poiščimo večkratnike našega primera, 12 in 8. Kaj je najmanjše število, ki jima je skupno? 24. 8, 16, 24 in 12, 24 - bingo

Korak 3. Pomnožite števec in imenovalec, da poiščete enakovreden ulomek
Oba imenovalca je treba spremeniti v 24. Kako pretvorite 12 v 24? Pomnožite z 2. 8 na 24? Pomnožite s tremi. Ampak ne pozabite - tudi števce morate pomnožiti!
Torej (13 x 2)/(12 x 2) = 26/24. In (17 x 3)/(8 x 3) = 51/24. S tem smo skoraj končali

Korak 4. Dodajte ali odštejte svoje ulomke
Zdaj, ko imate isti imenovalec, lahko preprosto dodate dva števca skupaj. Ne pozabite, samo pustite imenovalec!
26/24 + 51/24 = 77/24. To je vaša vsota! Vendar so bile številke na vrhu prevelike …

Korak 5. Pretvorite svoj odgovor nazaj v mešane številke
Zelo veliko število na vrhu ulomka se zdi nekoliko čudno - ne morete reči velikosti vašega ulomka. Vse, kar morate storiti, je, da od števca večkrat odštejete imenovalec, dokler ga ne morete več odšteti, in zapišite preostanek.
-
V tem primeru 77 minus 24 krat 3 -krat. To pomeni, da je 24 x 3 = 72. Preostanek je 5! Kakšen je torej vaš končni rezultat? 3 5/24.
Tako res!
Metoda 4 od 4: Dodajanje in odštevanje ulomkov brez iskanja LCM
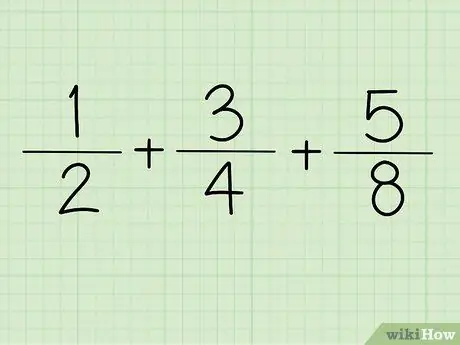
Korak 1. Zapišite ulomek
Na primer + +

Korak 2. Najprej rešite števec
- Pomnožite s števcem drugega ulomka.
- Pomnožite 1 s 4 in 8. [32]
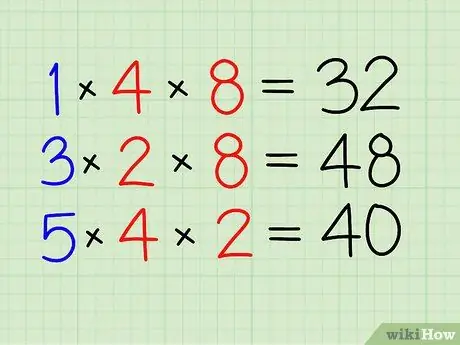
Korak 3. Enako storite z drugimi ulomki
- Pomnožite 3 z 2 in 8. [48]
- Na koncu pomnožite 5 s 4 in 2. [40]
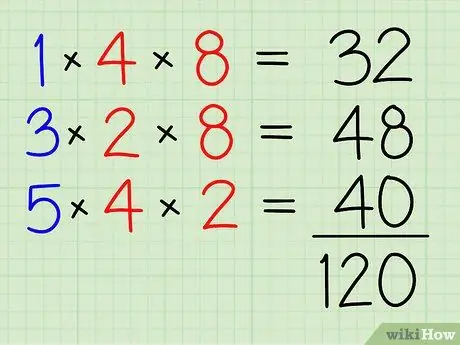
Korak 4. Dodajte jih vse skupaj
32+48+40=120
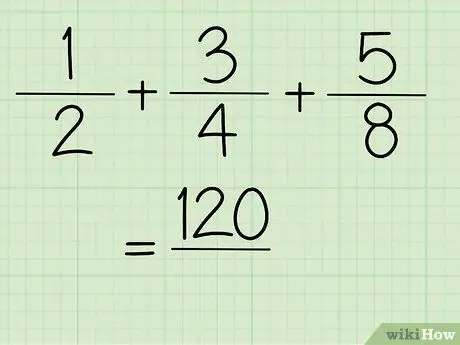
Korak 5. Zdaj dobite vrednost števca

Korak 6. Rešite imenovalec ulomka

Korak 7. Pomnožite vse imenovalce ulomkov
2×4×8=64

Korak 8. Zdaj dobite rezultat
120/64 = 1 56/64 = 1 ⅞
Opozorilo
- Ta metoda vam omogoča množenje velikih števil.
- Za izračun na ta način boste morda potrebovali kalkulator.






