- Avtor Jason Gerald [email protected].
- Public 2024-01-19 22:14.
- Nazadnje spremenjeno 2025-01-23 12:45.
Učenci, ki so še zelo mladi, imajo pogosto težave pri razumevanju pojma odštevanja. Če ste učitelj in želite učence učiti koncepta odštevanja, ga poskusite predstaviti na način, ki je za učence zanimiv in razumljiv. Ko razložite osnovne pojme odštevanja, poskusite preiti na pojem dvomestnega odštevanja. Ko ga učenci dobro obvladajo, poskusite razložiti različne koncepte, ki jih lahko uporabijo za reševanje težav odštevanja, na primer Common Core.
Korak
Metoda 1 od 4: Poučevanje odštevanja skozi predmete ali slike

Korak 1. Učencem napišite ali ustno predstavite problem zgodbe, ki vsebuje problem odštevanja:
Na mizi je 8 pomaranč, 3 pomaranče poje Jordan. Koliko pomaranč je ostalo?
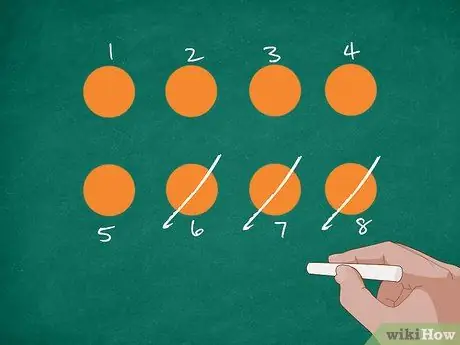
Korak 2. Predstavite težavo s slikami
Najprej na desko ali kos papirja narišite 8 oranžnih krogov. Po tem naj učenci preštejejo število in vsak krog označijo s številko. Prečrtajte 3 kroge in razložite, da je Jordan pojedel 3 pomaranče. Učence vprašajte, koliko pomaranč je zdaj ostalo.
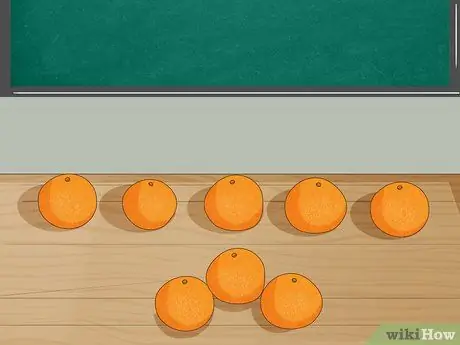
Korak 3. Predstavite težavo s predmeti
Na mizo postavite 8 pomaranč in učence prosite, naj preštejejo število. Nato vzemite 3 pomaranče z mize in pojasnite, da je Jordan pojedel 3 pomaranče. Učenci naj preštejejo število preostalih pomaranč.

Korak 4. Zapišite enačbo
Pojasnite, da je težave z zgodbo mogoče predstaviti tudi z enačbo. Vedno jih vodite pri spreminjanju zgodb v matematične enačbe.
- Vprašajte, koliko pomaranč je na mizi. Na tablo zapišite številko "8".
- Vprašajte, koliko pomaranč je Jordan pojedel. Na tablo zapišite številko "3".
- Učence vprašajte, ali gre za težavo seštevanja ali odštevanja. Med številkami »8« in »3« napišite znak »-«.
- Učenci naj poiščejo odgovore na enačbo »8-3«. Napišite znak »=«, ki mu sledi številka »5.«
Metoda 2 od 4: Poučevanje odštevanja z metodo odštevanja na številski črti

Korak 1. Učencem napišite ali ustno predstavite problem zgodbe, ki vsebuje problem odštevanja:
V trgovini za male živali je 10 psov, od katerih so jih 6 posvojili novi lastniki. Koliko psov ostane v trgovini za male živali?
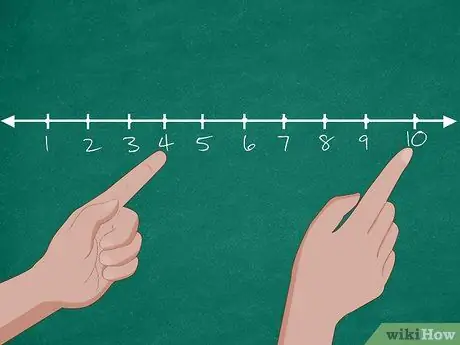
Korak 2. Za rešitev težave uporabite številčno črto
Najprej narišite številsko črto, ki vsebuje številke 0-10. Nato prosite študente, naj navedejo število psov v trgovini za male živali. Ko učenci odgovorijo, obkrožite številko »10« na tabli. Nato znova vprašajte, koliko psov je bilo posvojenih. Če učenci odgovorijo s "6", jih prosite, naj odštevajo 6 številk od 10 (9, 8, 7, 6, 5, 4), dokler ne dosežejo številke "4". Po tem ponovno vprašajte, koliko psov je ostalo v trgovini za male živali.

Korak 3. Zapišite enačbo
Pojasnite, da je težave z zgodbo mogoče predstaviti tudi z enačbo. Poskrbite, da jih boste vedno vodili pri spreminjanju zgodb v matematične enačbe.
- Vprašajte, koliko psov je v trgovini za male živali. Na tablo zapišite številko "10".
- Vprašajte, koliko psov je bilo posvojenih. Na tablo zapišite številko "6".
- Učence vprašajte, ali gre za težavo seštevanja ali odštevanja. Med številkami »10« in »6« napišite znak »-«.
- Učenci naj poiščejo odgovore na enačbo "10-6". Napišite znak »=«, ki mu sledi številka »4.«
Metoda 3 od 4: Poučevanje odštevanja skozi koncepte družine dejstev

Korak 1. Učencem predstavite koncept družine dejstev
Pravzaprav je družina dejstev skupina matematičnih problemov, sestavljenih iz istih številk. Na primer, številke 10, 3 in 7 tvorijo družino dejstev. Tri številke je mogoče seštevati ali odštevati na različne načine; Dve enačbi lahko ustvarite samo s temi tremi številkami:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

2. korak Učencem napišite ali ustno predstavite problem zgodbe, ki vsebuje problem odštevanja:
Imam 7 bonbonov. Koliko sladkarij ostane, če pojem 3 bonbone?

Korak 3. Za rešitev problema uporabite koncept družine dejstev
Učence vodite skozi postopek korak za korakom:
- Učence vprašajte, kateri problem bi radi rešili. Napišite "7-3 =?" na tablo.
- Prosite jih, naj identificirajo tretjega člana družine dejstev. Na tablo zapišite naslednje enačbe: “3+_ = 7”; "_+3 = 7"; "; "7 -_ = 3"; in 7-3 = _”Nato prosite učence, naj preberejo rezultate in problem napolnijo z odgovori, ki so jih dali.
Metoda 4 od 4: Predstavitev skupnih osnovnih konceptov
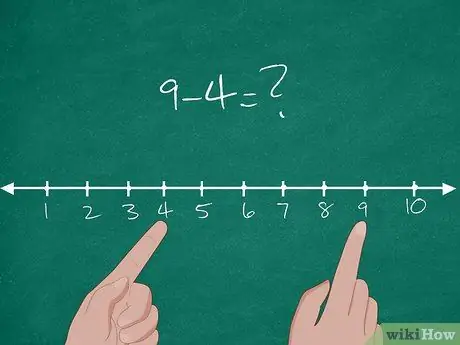
Korak 1. Naučite se koncepta odštevanja v skupnem jedru
Pravzaprav je Common Core nov učni standard, ki ga uporablja večina držav v Ameriki. V skupnem jedru je osnovni pojem odštevanja razložen z razdaljo med dvema številkama. Če želite učencem razložiti koncept, na tablo narišite številsko črto, ki vsebuje številke 1-10.
- Nato učencem zadamo osnovni problem odštevanja: 9-4 = ?.
- Poiščite lokacijo številke 4 v številski vrstici. Učencem razložite, da je ta lokacija njihovo izhodišče.
- Poiščite lokacijo številke 9 v številski vrstici. Učencem razložite, da je lokacija končni cilj.
- Nato prosite študente, da izmerijo ali izračunajo razdaljo med dvema številkama: "5, 6, 7, 8, 9."
- Razdalja med dvema številkama je 5. Tako je 9-4 = 5.
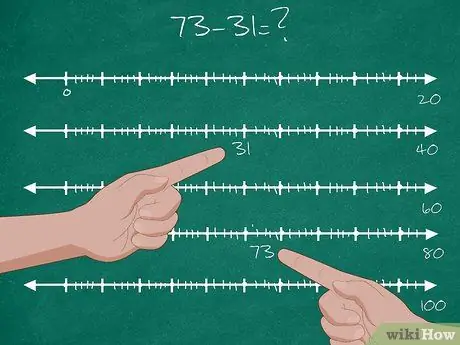
2. korak. Učenci naj rešijo dvomestno nalogo odštevanja
Učencem razložite, da se morata ustaviti pred prihodom na cilj.
- Dijakom dajte dvomestno težavo odštevanja: 73-31 = ?.
- Na številčni vrstici poiščite lokacijo številke 31. To je izhodišče.
- Poiščite lokacijo številke 73 v številski vrstici. To je končni cilj.
- »Ustavi se« v prvi desetinki po 31. Tako je vaša prva postaja 40. Nato izmerite razdaljo med 31 in 40 in zapišite odgovor: 9.
- "Ustavite se" pri desetih, ki so bližje 73. Tako je vaš drugi postanek 70. Nato izmerite razdaljo med 40 (prvi postanek) in 70 (drugi postanek) in zapišite odgovor: 30.
- "Premakni se" od 70 (druga postaja) do končnega cilja (73). Izmerite razdaljo med njimi in zapišite odgovor: 3.
- Dodajte te tri rezultate skupaj: 9+30+3 = 42. Tako je 73-31 = 42.

Korak 3. Učenci naj rešijo trimestno nalogo odštevanja
Pri reševanju dvomestnih težav odštevanja učencem razložite, da se ne bodo povečali le postanki, ampak tudi razdalja med vsakim postankom.
- Učencem podajte trimestni problem odštevanja: 815-398 = ?.
- Poiščite lokacijo številke 398 v številski vrstici. To je izhodišče.
- Poiščite lokacijo številke 815 v številski vrstici. To je končni cilj.
- "Ustavi se" na prvi desetini po 398. Tako je vaša prva postaja 400. Izmerite razdaljo med 398 in 400 in zapišite odgovor: 2.
- "Ustavite se" pri desetih, ki so bližje številki 815. Vaš drugi postanek je torej 800. Izmerite razdaljo med 400 in 800 in zapišite odgovor: 400.
- "Ustavite se" pri desetih, ki so bližje 815. Tako je vaš tretji postanek 810. Izmerite razdaljo med 800 in 810 in zapišite odgovor: 10.
- "Premakni se" od tretje postaje do cilja, ki je številka 815. Izmerite razdaljo in zapišite odgovor: 5.
- Dodajte vse številke, ki jih dobite: 2+400+10+5 = 417. Tako 815-398-417.






