Matrica je pravokotna razporeditev števil, simbolov ali izrazov v vrsticah in stolpcih. Če želite pomnožiti matriko, morate elemente (ali številke) v prvi vrstici matrice pomnožiti z elementi v drugi vrstici matrice in sešteti zmnožek. Matrice lahko pomnožite z le nekaj preprostimi koraki, ki zahtevajo pravilno seštevanje, množenje in umestitev rezultatov.
Korak
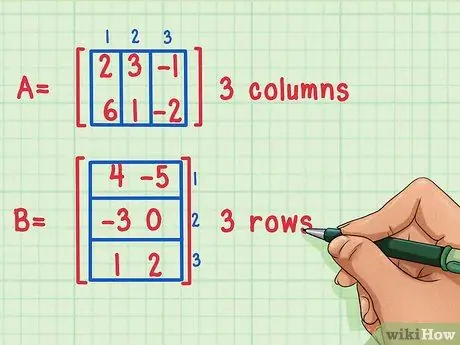
Korak 1. Poskrbite, da se matrice množijo
Matrico lahko pomnožite le, če je število stolpcev prve matrike enako številu vrstic druge matrike.
Te matrike je mogoče pomnožiti, ker ima prva matrika, matrika A, 3 stolpce, druga matrika, matrika B, pa 3 vrstice
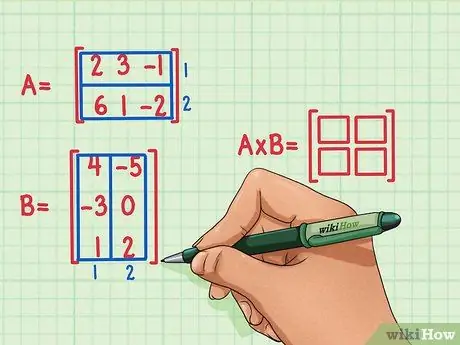
Korak 2. Označite dimenzije matričnega izdelka
Ustvarite novo, prazno matriko, ki bo označevala dimenzije produkta dveh matrik. Matrika, ki predstavlja produkt matrike A in matrike B, bo imela enako število vrstic kot prva matrika in enako število stolpcev kot druga matrika. Če želite prikazati število vrstic in stolpcev v tej matrici, lahko narišete prazna polja.
- Matrika A ima 2 vrstici, zato bo rezultat množenja matrike imel 2 vrstici.
- Matrika B ima 2 stolpca, zato bo rezultat množenja matrike 2 stolpca.
- Rezultat matričnega produkta bo imel 2 vrstici in 2 stolpca.
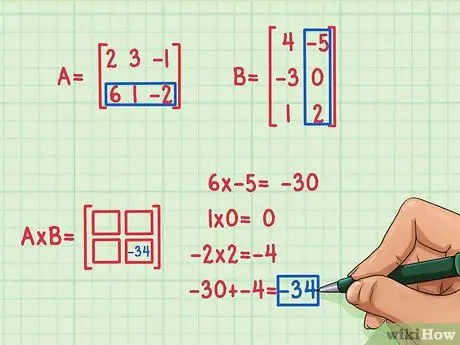
Korak 3. Poiščite rezultat prvega pikčastega izdelka
Če želite najti rezultat prvega pikčastega izdelka, morate prvi element v prvi vrstici pomnožiti s prvim elementom v prvem stolpcu, drugi element v prvi vrstici z drugim elementom v prvem stolpcu in tretji element v prvo vrstico s tretjim elementom v prvem stolpcu. Nato seštejte rezultate množenja, da jih poiščete pikčast izdelek (pika).
Recimo, da ste se odločili najprej izračunati elemente v drugi vrstici in drugem stolpcu (spodaj desno) matričnega produkta. To storite tako:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Rezultat pikčastega produkta je -34 in ta rezultat je zapisan v spodnjem desnem kotu matričnega produkta.
Ko pomnožite matriko, se bo pikčasti zmnožek zapisal v položaj vrstice prve matrice in položaj stolpca druge matrice. Ko na primer poznate pikčasti zmnožek spodnje vrstice matrike A in desnega stolpca matrike B, je odgovor -34 zapisan v spodnjo vrstico in desni stolpec matričnega produkta
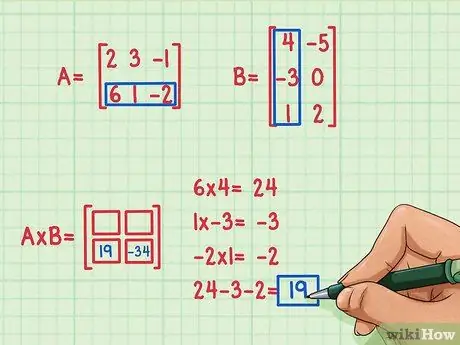
Korak 4. Poiščite rezultat drugega pikčastega izdelka
Recimo, da želite izraz poiskati v spodnjem levem kotu matričnega produkta. Če želite najti ta izraz, morate le pomnožiti elemente v spodnji vrstici prve matrike z elementi v prvem stolpcu druge matrice in jih nato sešteti. Uporabite isto metodo kot množenje prve vrstice in stolpca - znova poiščite pikčasti izdelek (ne t)njegova.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Rezultat pikčastega produkta je -19 in ta rezultat je zapisan v spodnjem levem kotu matričnega produkta.
Korak 5. Poiščite druga dva izdelka s pikami
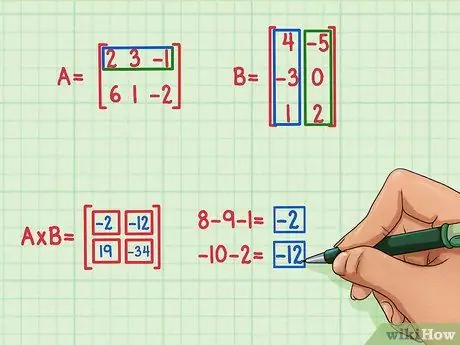
Če želite poiskati izraz v zgornjem levem kotu matričnega produkta, začnite z iskanjem točkovnega produkta zgornje vrstice matrike A in levega stolpca matrike B. To storite tako:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Rezultat pikčastega produkta je -2 in ta rezultat je zapisan v zgornjem levem kotu matričnega produkta.
Če želite poiskati izraz v zgornjem desnem kotu matričnega produkta, poiščite pikčasti produkt zgornje vrstice matrike A in desnega stolpca matrike B. To storite tako:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Točkast produkt je -12 in ta rezultat je zapisan v zgornjem desnem kotu matričnega produkta.
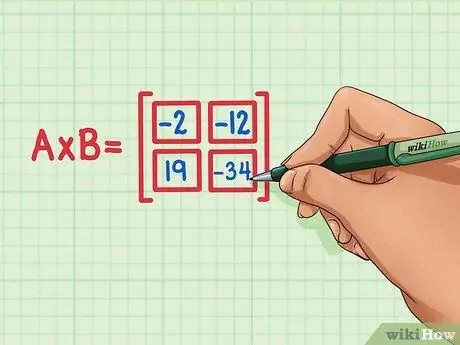
Korak 6. Prepričajte se, da so izdelki s štirimi pikami na pravilnem mestu v matričnem izdelku
19 mora biti spodaj levo, -34 mora biti spodaj desno, -2 mora biti zgoraj levo in -12 mora biti zgoraj desno.
Nasveti
- Z uporabo segmentnih vrstic in ne z uporabo vrstic lahko dobite napačen odgovor. Če vrstica, ki predstavlja vrstico, zahteva razširitev, da prečka stolpec, jo podaljšajte! To je samo tehnika vizualizacije, da boste lažje vedeli, katere vrstice in stolpce uporabite za delo z vsakim elementom izdelka.
- Zmnožek dveh matrik bo ustvaril število vrstic, ki je enako številu vrstic prve matrice in število stolpcev, ki je enako številu stolpcev druge matrike.
- Zapišite vsoto. Množenje matric vključuje veliko izračunov in zelo enostavno se je mogoče izogniti in pozabiti, katero število množite.
