- Avtor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- Nazadnje spremenjeno 2025-01-23 12:44.
Mestna vrednost ali koncept, da je vrednost števila (0-9) določena z njegovim položajem v določenem številu, je temeljni pojem v matematiki. Ker je ta koncept tako preprost za ljudi, ki ga že razumejo, je poučevanje lahko precej zapleteno. Ko pa bodo učenci dojeli ta koncept, bodo pripravljeni in navdušeni, da uporabijo svoje nove sposobnosti in se naučijo bolj zapletenih matematičnih konceptov.
Korak
1. del od 3: Predstavitev osnovnih konceptov

Korak 1. Vzemite si čas, da poučite vrednost mesta
Če poučujete v okviru vnaprej določenega učnega načrta, bi morali že imeti idejo, kako umestiti vrednost v širši obseg učenja. Če učite ali učite doma, bo učna struktura bolj prilagodljiva. Načrtujte poučevanje vrednosti mesta nekoč, ko se učenci končajo z učenjem štetja in izvajajo preproste operacije seštevanja in odštevanja - običajno okoli prvega ali drugega razreda. Razumevanje vrednosti kraja bo tem otrokom omogočilo razumevanje bolj zapletenih matematičnih konceptov.

Korak 2. Predstavite koncept štetja skupin števil
Večina učencev otrok se nauči šteti le eno za drugo: ena … dve … tri … štiri. To zadošča za osnovno seštevanje in odštevanje, vendar še vedno preveč preprosto, da bi zagotovilo trdno podlago za razumevanje kompleksnejših funkcij. Preden jih naučite, kako razčleniti velika števila na ustrezne mestne vrednosti, je dobro, da jih naučite razdeliti skupino majhnih številk na velika.
- Naučite svoje učence, kako šteti dva dva, tri tri, pet pet in deset deset. To je temeljni koncept, ki ga morajo študentje razumeti, preden spoznajo vrednost kraja.
- Zlasti poskusite zgraditi močno "vznemirjenje deset". Sodobna matematika uporablja številko deset kot osnovo, zato se otroci lažje naučijo kompleksnejših sistemov, če se navadijo razmišljati na ta način. Naučite svoje učence, da nagonsko združijo številke v deset.

Korak 3. Preglejte koncept vrednosti mesta
Osvežite svoje razumevanje. Poskusite sami popolnoma razumeti ta koncept, preden ga poskusite naučiti skupino mladih študentov. Preprosto povedano, vrednost mesta je ideja, da je vrednost števila (0-9) odvisna od njegovega "mesta" ali položaja v številki.

Korak 4. Razložite razliko med številkami in številkami
Številke so simboli desetih osnovnih števil, ki sestavljajo vsa števila: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Te številke so združene, da tvorijo vsa druga števila. Številka je lahko številka (npr. Številka 7), vendar le, če ni združena z drugimi številkami. Ko sta dve ali več števil združeni, zaporedje števil tvori večje število.
Pokažite, da je samo "1" številka ena, "7" pa številka sedem. Ko sta združeni kot "17", dve številki tvorita številko sedemnajst. Podobno "3" in "5" skupaj tvorita številko petintrideset. Pokažite še nekaj primerov, da se bodo učenci razumeli
2. del 3: Poučevanje z vizualnimi primeri
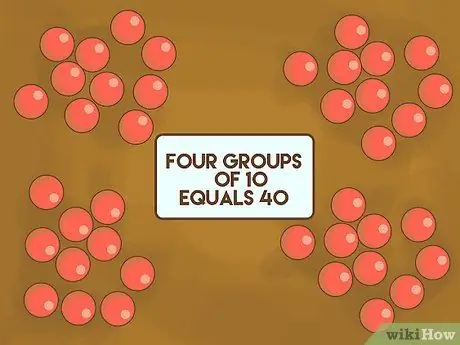
Korak 1. Otrokom pokažite, da je lažje šteti deset do deset
Uporabite 30-40 predmetov, ki so majhni, šteti in dokaj homogeni. Na primer: kamenčki, frnikole ali radirka. Razširite ga na mizo pred učenci. Pojasnite, da v sodobni matematiki za osnovo uporabljamo številko 10. Predmete razporedite v več skupin, nato jih preštejte pred razredom. Pokažite jim, da štiri skupine po 10 kamenčkov ustrezajo 40.

Korak 2. Primer s kamenčki prevedite v zapisane številke
Konceptno skico napišite na tablo. Najprej ustvarite navaden T-diagram. V zgornji desni kot grafikona T zapišite številko 1. Nato v zgornji levi vnesite številko 10. V stolpec na desni z oznako "1" vnesite 0, v stolpec na levi strani z oznako "10" pa 4. Zdaj lahko razredu razložite, da ima vsaka številka s kamenčki svoje "mesto".
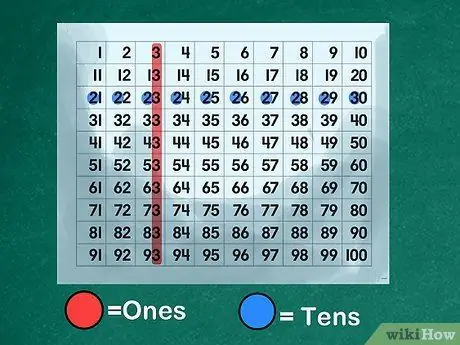
Korak 3. S številsko tipkovnico ponazorite osnovo vrednosti mesta
Ustvarite ali natisnite "številčnico", ki prikazuje vse številke v vrstnem redu od 1 do 100. Pokažite učencem, kako številke od 0 do 9 delujejo s številkami od 10 do 100. Pojasnite, da je vsaka številka od 10 do 99 sestavljena iz dveh številk., ena številka na mestu "ena" in druga številka na mestu "desetke". Pokažite, da številka "4" predstavlja "štiri", ko je na mestu "ena", vendar služi kot predpona za številko "40", ko je na mestu "desetice".
- Ponazorite kraj "enot". Usmerite razred, da poimenuje vse številke, ki imajo na mestu "ena" številko "3": 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Pojasnite mesto "desetice". Naredite učencem, naj označijo vsa števila, ki imajo "2" namesto "deset": 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Pojasnite, da je "3" v "23" zložene na vrhu "20", označene s številko "2." Naučite svoje otroke, da preberejo kraj "desetice" kot sprožilec za učenje.

Korak 4. Poskusite z drugimi vizualnimi učnimi orodji
Lahko uredite fizične predmete ali jih narišete na tablo. Vrednost mesta lahko razložite z uporabo prirastkov denarne vrednosti, ki so jih študentje morda že študirali, da jih povežete s pomanjšanimi numeričnimi vrednostmi. Za zabavno in interaktivno dejavnost poskusite uporabiti študente kot "skupinsko" vrednost.
V človeškem spominu prevladujejo vizualne stvari, zato je koncept mestne vrednosti še vedno abstrakten, dokler ga ne naredite vizualnega. Medtem so lahko sami številčni simboli za otroke še vedno abstraktni! Poiščite načine za oblikovanje štetja skupin in določite vrednostne dejavnosti tako, da bodo preproste, oprijemljive in intuitivne
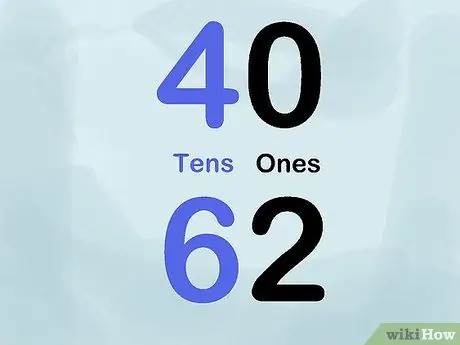
Korak 5. Uporabite barvo
Poskusite uporabiti kredo ali označevalce različnih barv za prikaz vrednosti mesta. Na primer, napišite različne številke s črnim označevalcem za mesto "ena" in modrim označevalcem za mesto "desetke". Tako bi napisali 40 s številko "4" v modri barvi in številko "0" v črni barvi. Ta trik ponovite za veliko število številk, da prikažete uporabo vrednosti mesta na plošči.
3. del 3: Uporabite interaktivne primere
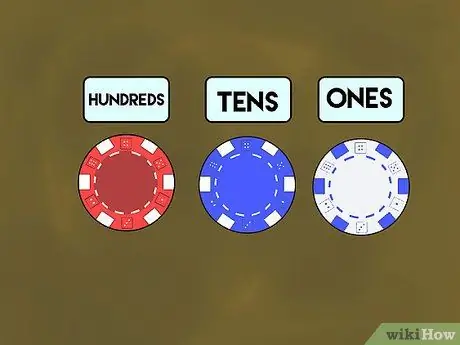
Korak 1. Poučite s poker žetoni
Najprej razdelite poker žetone vsakemu študentu. Povejte jim, da beli žetoni predstavljajo mesto "tistih", modri čipi za "desetke", rdeči pa "stotine". Nato svojim učencem pokažite, kako z uporabo mestnih vrednosti v obliki pisanih žetonov narediti številke. Poimenujte številko (recimo 7) in postavite beli čip desno od mize.
- Poimenujte drugo številko - na primer 30. Postavite tri modre žetone, ki predstavljajo 3 (na mestu "desetice") in nič belih žetonov, ki predstavljajo 0 (na mestu "ena").
- Ni vam treba uporabljati poker žetonov. Za predstavitev treh osnovnih vrednosti "mesta" lahko uporabite kateri koli predmet, če je vsaka skupina (barva čipov itd.) Standardna, homogena in zlahka prepoznavna.

Korak 2. Naredite učencem, da si med seboj izmenjujejo kose
Ta metoda lahko ponazori nizke vrednosti mest, ki sestavljajo višje vrednosti mest. Ko študentje dobro razumejo vrednost mesta, poučite svoj razred, kako zamenjati bele "ene" žetone za modre "desetice" žetone, nato pa "desetke" žetone zamenjajte za "stotine". Učence vprašajte: "Koliko modrih žetonov dobim z zamenjavo 16 belih žetonov? Če zamenjam tri modre žetone, koliko belih žetonov dobim?"

Korak 3. Pokažite, kako narediti seštevanje in odštevanje s poker žetoni
Tega koncepta se je mogoče naučiti šele, ko študentje obvladajo izmenjavo poker žetonov. Koristno je začeti s pisanjem primera.
- Za osnovno težavo pri seštevanju naj učenci položijo tri modre žetone (desetice) in šest belih žetonov (ena). Učence vprašajte o številkah, nastalih s čipi. (Odgovor je 36!)
- Delajte na isti številki. Vaši učenci naj številki 36 dodajo pet belih žetonov. Vprašajte jih o trenutni številki. (Odgovor je 41!) Nato vzemite modri čip in jih vprašajte o trenutni številki. (Odgovor je 31!)






