Geometrijska sredina je še en način za določanje povprečne vrednosti niza števil, ki se izvede tako, da se vrednosti pomnožijo, preden se vzamejo korenine, namesto da se vrednosti seštevajo in delijo kot v aritmetični sredini. Geometrijsko sredino lahko uporabimo za izračun povprečne stopnje donosa v finančni analizi ali za prikaz stopnje rasti nečesa v določenem časovnem obdobju. Če želite najti geometrijsko sredino, pomnožite vse vrednosti pred ukoreninjenjem s, kar je skupno število številk v nizu. Če želite, lahko uporabite tudi funkcijo logaritma v svojem kalkulatorju za iskanje geometrijske sredine.
Korak
Metoda 1 od 2: Iskanje geometrijskega povprečja niza vrednosti
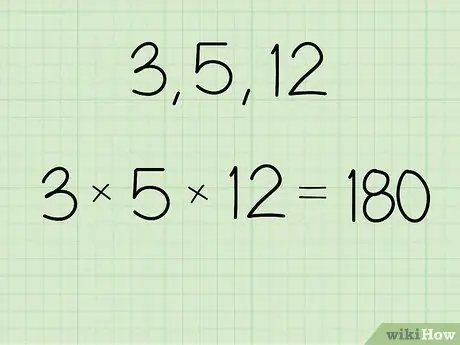
Korak 1. Pomnožite vrednost, za katero želite najti geometrijsko sredino
Če želite dobiti rezultat, lahko uporabite kalkulator ali računate ročno. Zapišite si rezultate, da ne pozabite.
- Na primer, če je niz števil 3, 5 in 12, izračunajte: (3 x 5 x 12) = 180.
- Za drug primer, če želite najti geometrijsko sredino niza števil 2 in 18, napišite: (2 x 18) = 36.
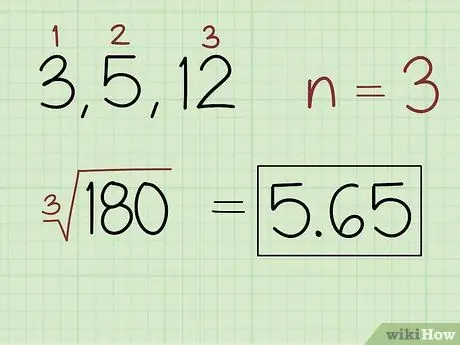
Korak 2. Poiščite n -ti koren izdelka, kjer je n število vrednosti v nizu
Preštejte število številk v nizu, da dobite vrednost. Z vrednostmi določite koren, ki ga je treba uporabiti v izdelku. Na primer, uporabite kvadratni koren, če niz vsebuje 2 številki, kubični koren, če niz vsebuje 3 številke itd. Za izračun enačbe uporabite kalkulator in zapišite odgovor.
- Na primer za niz številk 3, 5 in 12 napišite: (180) 5, 65.
- V drugem primeru z nizom, ki vsebuje 2 in 18, napišite: (36) = 6.
Različica:
Koren lahko zapišete tudi kot eksponent 1/, če je lažje pisati v kalkulatorju. Na primer za niz številk 3, 5 in 12 napišite (180)1/3 namesto (180).
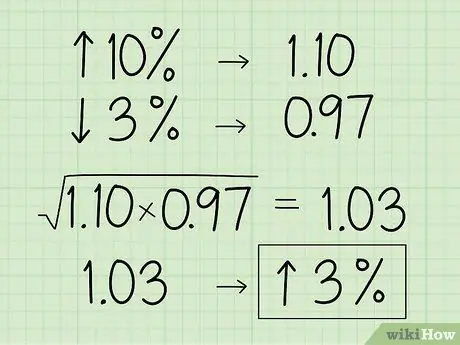
Korak 3. Pretvorite odstotek v ekvivalent decimalnega množitelja
Če je niz številk zapisan kot povečanje ali zmanjšanje odstotka, poskusite ne uporabljati vrednosti odstotka v geometrijski sredini, ker rezultati ne bodo točni. Če se odstotek poveča, premaknite decimalno vejico za dve števki v levo in dodajte 1. Če se odstotek zmanjša, premaknite decimalno vejico 2 števki v levo in odštejte od 1.
- Na primer, recimo, da želite najti geometrijsko sredino vrednosti objektov, ki se poveča za 10%, nato pa zmanjša za 3%.
- Pretvorite 10% v decimalno število in dodajte 1, da dobite 1, 10.
- Nato pretvorite 3% v decimalno število in odštejte 1, da dobite 0,97.
- Z obema decimalnima mestoma poiščite geometrijsko sredino: (1, 10 x 0,97) 1,03.
- Pretvorite število nazaj v odstotek tako, da decimalno vejico premaknete za 2 števki v desno in odštejete 1, da dobite 3 -odstotno povečanje vrednosti.
Metoda 2 od 2: Izračun geometrijskega povprečja z uporabo logaritmov
Korak 1. Seštejte logaritmične vrednosti za vsako število v nizu
Funkcija LOG v kalkulatorju vzame osnovo 10 števila in določi, koliko morate pomnožiti z 10, tako da je enako številki. Na kalkulatorju poiščite funkcijo LOG, ki je običajno na levi strani gumba. Kliknite gumb LOG in vnesite prvo številko v nizu. Pred vnosom LOG za drugo številko vnesite “+”. Še naprej ločite funkcijo LOG za vsako številko s simbolom plus, preden dobite vsoto.
- Na primer, za sklope 7, 9 in 12 vnesite log (7) + log (9) + log (12), nato pritisnite “=” na kalkulatorju. Če je funkcija izračunana, bo število okoli 2,878521796.
- Prav tako lahko izračunate vsak logaritem posebej, preden jih dodate skupaj.
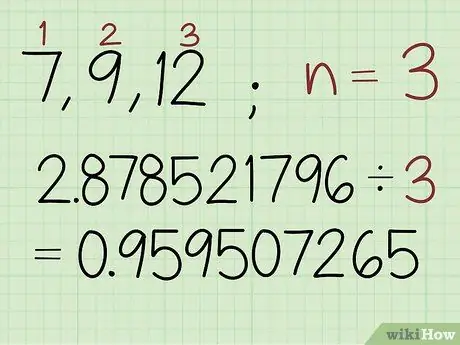
Korak 2. Vsoto logaritemskih vrednosti delite s številom številk v nizu
Preštejte število vrednosti v nizu in prej pridobljeno število delite s tem številom. Rezultat je logaritem geometrijske sredine.
V tem primeru so v nizu 3 številke, zato vnesite: 2, 878521796 /3 0, 959507265
Korak 3. Poiščite antilog količnika za določitev geometrijske sredine
Funkcija antilog je obratno od funkcije LOG na kalkulatorju in vrednost pretvori nazaj v osnovo 10. Poiščite simbol “10x”Na kalkulatorju, kar je običajno sekundarna funkcija gumba LOG. Pritisnite gumb »2nd« v zgornjem levem kotu kalkulatorja, nato pa gumb LOG, da aktivirate antilog. Preden rešite enačbo, vnesite količnik, ki ste ga našli v zadnjem koraku.
V tem primeru bo kalkulator prikazal: 10(0, 959507265) ≈ 9, 11.
Nasveti
- Ne najdete geometrijske sredine negativnih števil.
- Vsi nizi, ki imajo 0, bodo imeli geometrijsko sredino 0.
